In this article we will discuss dot multiplication which produces scalar and cross multiplication which produces vector magnitude , along with Questions and Solutions dot multiplication and vector cross multiplication.
A. Multiplication of Dot (.)
Example vector $ \vec{A} = (A_i+ A_j+ A_k ) $ and vektor $ \vec{B} = (B_i+ B_j+B_k ) $ wherein the two vectors forming an angle of θ, so:
$\vec{A} . \vec{B} = |\vec{A}||\vec{B}| \cos \theta $
with:
$\small \begin{align*} \left |A \right | &= \sqrt{A_i^2+A_j^2+A_k^2}\\\left |B \right | &= \sqrt{B_i^2+B_j^2+B_k^2}\end{align*}$
Dot Multiplication (dot multiplication) Algebraically
$ \vec{A} . \vec{B} = A_i.B_i + A_j.B_j + A_k.B_k $
dot multiplication result:
$\begin{align*}i . i &= j . j = k . k = 1\\i . j &= j . k = j . k = 0\end{align*}$
B. Multiplication Cross ($\times $)
In cross multiplication, the symbol 'x' is used. Let vector $\vec {A} = (A_i+ A_j+A_k)$ and vektor $ \vec {B} = (B_i+ B_j+ B_k)$. so:
$\begin{align*}A \times B = \left | A \right |\left | B \right |\sin\theta \end{align*}$
with:
$\small \begin{align*} \left |A \right | &= \sqrt{A_i^2+A_j^2+A_k^2}\\\left |B \right | &= \sqrt{B_i^2+B_j^2+B_k^2}\end{align*}$
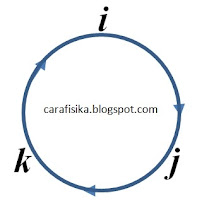
To make it easier for friends to understand the Cross Operation ($\times $), see the picture below, in the direction of the positive arrow, opposite the negative arrow.Thus we can write:
\begin{align*}i \times j &= +k\textrm{, } j \times i =-k\\k \times i &= +j\textrm{, }i \times k =-j\\j \times k&=+ i \textrm{, }k \times j = -i\\&\textrm{with:}\\i \times i &= j \times j = k\times k = 0\end{align*}
C. Dot and Cross Multiplication Questions and Solutions
Problem: 1. Know the vector $ \vec{A} = (3, -5, 4) $ and $ \vec{B} = (-2,1,2).$ . Find the sine of the angle between the vectors $ \vec{A} $ and $ \vec{B}$! !
Vector solution:
angle value:
$\small \begin{align} \cos \theta & = \frac{ \vec{A} . \vec{B} }{|\vec{A}||\vec{B}| } \\ & = \frac{ -6 - 5 + 8 }{\sqrt{3^2 + (-5)^2 + 4^2} . \sqrt{(-2)^2 + 1^2 + 2^2} } \\ & = \frac{ -3 }{\sqrt{50} . \sqrt{9} } = \frac{ -3 }{5\sqrt{2} .3 } \\ & = \frac{ -1 }{5\sqrt{2} } \end{align} $
With the formula of trigonometric identity $\sin ^2 \theta + \cos ^2 \theta = 1$ , so:$\begin{align*} \sin ^2 \theta &+ \cos ^2 \theta = 1 \\ \sin ^2 \theta & = 1 - \cos ^2 \theta \\ \sin \theta & = \sqrt{ 1 - \cos ^2 \theta } \\ & = \sqrt{ 1 - ( \frac{ -1 }{5\sqrt{2} } )^2 } \\ & = \sqrt{ 1 - \frac{1 }{50} } \\ & = \sqrt{ \frac{49 }{50} } \\ & = \frac{7}{5\sqrt{2}} =0,7\sqrt{2} \end{align*}$
Problem: 2. Given a vector:
Since $ \vec{A} $ is perpendicular to $ \vec{C} $ , then $ \vec{A}.\vec{C} = 0 $.
a. Value $ \vec{A} (\vec{B} + \vec{C}) $
$\small \begin{align} \vec{A} (\vec{B} + \vec{C}) & = \vec{A} . \vec{B} + \vec{A}. \vec{C} \\ & = |\vec{A}| |\vec{B} | \cos 60^\circ + 0 \\ & = 4. 3. \frac{1}{2} \\ & = 6 \end{align} $
b. Value $ \vec{A}(2\vec{C} - 3\vec{B}) $
$\small \begin{align} \vec{A}(2\vec{C} - 3\vec{B}) & = 2(\vec{A}.\vec{C}) - 3(\vec{ A}.\vec{B}) \\ & = 2.0 - 3|\vec{A}| |\vec{B} | \cos 60^\circ \\ & = 0 - 3 . 4. 3. \frac{1}{2} \\ & = - 18 \end{align} $
$\small \begin{align} \cos \theta & = \frac{ \vec{A} . \vec{B} }{|\vec{A}||\vec{B}| } \\ & = \frac{ -6 - 5 + 8 }{\sqrt{3^2 + (-5)^2 + 4^2} . \sqrt{(-2)^2 + 1^2 + 2^2} } \\ & = \frac{ -3 }{\sqrt{50} . \sqrt{9} } = \frac{ -3 }{5\sqrt{2} .3 } \\ & = \frac{ -1 }{5\sqrt{2} } \end{align} $
With the formula of trigonometric identity $\sin ^2 \theta + \cos ^2 \theta = 1$ , so:$\begin{align*} \sin ^2 \theta &+ \cos ^2 \theta = 1 \\ \sin ^2 \theta & = 1 - \cos ^2 \theta \\ \sin \theta & = \sqrt{ 1 - \cos ^2 \theta } \\ & = \sqrt{ 1 - ( \frac{ -1 }{5\sqrt{2} } )^2 } \\ & = \sqrt{ 1 - \frac{1 }{50} } \\ & = \sqrt{ \frac{49 }{50} } \\ & = \frac{7}{5\sqrt{2}} =0,7\sqrt{2} \end{align*}$
Problem: 2. Given a vector:
$\begin{align*} \vec{A} &= (2i + 3j-4k) \\\vec{B}&= (i-2j + 3k) \\ \vec{C} &= (i-10j-7k)\end{align*}$
so $\vec{A} \times \vec{B}$ dan $(\vec{A} \times \vec{B}) \times \vec{C}$ is...
Vector solution:
$\small \begin{align*} \vec{A} \times \vec{B} &= (2i + 3j-4k) \times (i-2j + 3k) \\=&-4k-6j-3k + 9i-4j-8i\\=& i-10j-7k\\ (\vec{A} \times \vec{B}) &\times \vec{C} = (i-10j-7k)\times (i-j+k)\\ =&-k-j + 10k-10i-7j-7i \\=&-17i-8j + 9k \end{align*}$
A, B, C = besar vektor A, B, C
i, j, k = unit vector for the x, y, z axes
Problem: 3. If vectors $ \vec{A} $ and $ \vec{B} $ form an angle of 60 , and vector $ \vec{A} $ is perpendicular to vector $ \vec{C} $ , with$ |\vec{A}| = 4 $ , $ |\vec{B}| = 3 $ , dan $ |\vec{C}| = 6 $, then specify:
A, B, C = besar vektor A, B, C
i, j, k = unit vector for the x, y, z axes
Problem: 3. If vectors $ \vec{A} $ and $ \vec{B} $ form an angle of 60 , and vector $ \vec{A} $ is perpendicular to vector $ \vec{C} $ , with$ |\vec{A}| = 4 $ , $ |\vec{B}| = 3 $ , dan $ |\vec{C}| = 6 $, then specify:
- $ \vec{A} (\vec{B} + \vec{C}) $
- $ \vec{A}(2\vec{C} - 3\vec{B}) $
Since $ \vec{A} $ is perpendicular to $ \vec{C} $ , then $ \vec{A}.\vec{C} = 0 $.
a. Value $ \vec{A} (\vec{B} + \vec{C}) $
$\small \begin{align} \vec{A} (\vec{B} + \vec{C}) & = \vec{A} . \vec{B} + \vec{A}. \vec{C} \\ & = |\vec{A}| |\vec{B} | \cos 60^\circ + 0 \\ & = 4. 3. \frac{1}{2} \\ & = 6 \end{align} $
b. Value $ \vec{A}(2\vec{C} - 3\vec{B}) $
$\small \begin{align} \vec{A}(2\vec{C} - 3\vec{B}) & = 2(\vec{A}.\vec{C}) - 3(\vec{ A}.\vec{B}) \\ & = 2.0 - 3|\vec{A}| |\vec{B} | \cos 60^\circ \\ & = 0 - 3 . 4. 3. \frac{1}{2} \\ & = - 18 \end{align} $
Hope it is useful. regards..!