More precisely, the energy per unit charge for the test charge is so small that the field disturbance under consideration can be neglected.
Furthermore, the motion across the field should be continued with negligible acceleration, to avoid the test charge gaining kinetic energy or generating radiation. By definition, the electric potential at the reference point is zero units.
Usually, the reference point is the earth or the infinity point, although any point can be used.
The electric potential arising from a point charge Q, at a distance r from the charge is:
${\displaystyle V_{\mathbf {E} }={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r}},}$
where 0 is the permittivity of the vacuum.
Problem 1: refer to a thin, nonconducting ring of radius R, as shown below, which has a charge Q uniformly spread out on it.
The electric potential at a point P, which is located on the axis of symmetry a distance x from the center of the ring, is given by A. $\frac{Q}{4\pi\epsilon _ox}$
B. $\frac{Q}{4\pi\epsilon _o\sqrt{(R^2 + x^2)}}$
C. $\frac{Qx}{4\pi\epsilon _o(R^2 + x^2)}$
D. $\frac{Qx}{4\pi\epsilon _o(R^2 + x^2)^{3/2}}$
E. $\frac{QR}{4\pi\epsilon _o(R^2 + x^2)}$
Problem 2: Two large conducting plates form a wedge of angle α as shown-in the diagram above. The plates are insulated from each other; one has a potential V0 and the other is grounded.
Furthermore, the motion across the field should be continued with negligible acceleration, to avoid the test charge gaining kinetic energy or generating radiation. By definition, the electric potential at the reference point is zero units.
Usually, the reference point is the earth or the infinity point, although any point can be used.
The electric potential arising from a point charge Q, at a distance r from the charge is:
${\displaystyle V_{\mathbf {E} }={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r}},}$
where 0 is the permittivity of the vacuum.
Problem 1: refer to a thin, nonconducting ring of radius R, as shown below, which has a charge Q uniformly spread out on it.

The electric potential at a point P, which is located on the axis of symmetry a distance x from the center of the ring, is given by A. $\frac{Q}{4\pi\epsilon _ox}$
B. $\frac{Q}{4\pi\epsilon _o\sqrt{(R^2 + x^2)}}$
C. $\frac{Qx}{4\pi\epsilon _o(R^2 + x^2)}$
D. $\frac{Qx}{4\pi\epsilon _o(R^2 + x^2)^{3/2}}$
E. $\frac{QR}{4\pi\epsilon _o(R^2 + x^2)}$
Electric Potential Solution:
Electric Potential, $\displaystyle V = \frac{kQ}{r}$
with $k=\frac{1}{4\pi\epsilon _o}$
The distance r of P from the charged ring is r2 = R2 + x2
$V=\frac{Q}{4\pi\epsilon _o\sqrt{(R^2 + x^2)}}$
with $k=\frac{1}{4\pi\epsilon _o}$
The distance r of P from the charged ring is r2 = R2 + x2
$V=\frac{Q}{4\pi\epsilon _o\sqrt{(R^2 + x^2)}}$
Answer: B
Problem 2: Two large conducting plates form a wedge of angle α as shown-in the diagram above. The plates are insulated from each other; one has a potential V0 and the other is grounded.
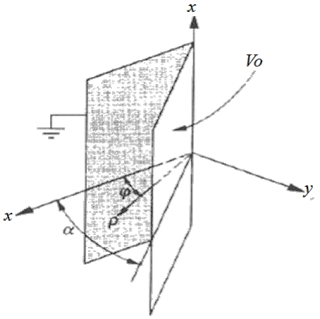
Assuming that the plates are large enough so that the potential difference between them is independent of the cylindrical coordinates z and ρ, the potential anywhere between the plates as s function of the angle φ is A. V0/α
B. V0φ/α
C. V0α/φ
D. V0φ2/α
E. V0α/φ2
Electric Potential Solution:
Boundary conditions:
V(φ = 0) = 0
V(φ = α) = V0
(A) FALSE
V0/α does not depend on φ
(B) TRUE
V0φ/α = 0 for φ = 0
V0φ/α = V0 for φ = α
(C) FALSE. V0α/φ = ∞ for φ = 0
For φ = α, V0φ2/α = V0α
Boundary conditions:
V(φ = 0) = 0
V(φ = α) = V0
(A) FALSE
V0/α does not depend on φ
(B) TRUE
V0φ/α = 0 for φ = 0
V0φ/α = V0 for φ = α
(C) FALSE. V0α/φ = ∞ for φ = 0
(D) FALSE
For φ = α, V0φ2/α = V0α
(E) FALSEFor φ = α, V0φ2/α = V0α
For φ = α, V0φ2/α = V0α
Answer: B