What is Electric Force?
Force in physics has a very specific meaning. In physics, a force is an interaction between two objects that has the ability to change the motion of one or both objects. One of the fundamental forces in the universe is the electric force. This is the force that exists between all charged particles.
Force in physics has a very specific meaning. In physics, a force is an interaction between two objects that has the ability to change the motion of one or both objects.
One of the fundamental forces of the universe is the electric force. This is the force that exists between all charged particles.
Coulomb's law states that the electric force between two charged objects is directly proportional to the product of the sum of the charges on the objects and inversely proportional to the square of the distance between them.
In equation form, Coulomb's law can be expressed as
\[F=k\frac{Q_1.Q_2}{r^2}\]where
Problem 1: Two balls of identical conductors, A and B, carry the same charge. The two are initially separated by a distance much larger than their diameter, and the force between them is F. The third identical conducting sphere, C, has no charge. Ball C is first touched to A, then to B, and then removed. Consequently, the force between A and B is equal to.
A. 0
B. $\displaystyle \frac{1}{6}F$
C. $\displaystyle \frac{1}{4}F$
D. $\displaystyle \frac{3}{8}F$
E. $\displaystyle \frac{1}{2}F$
Electric Force Solution:
Coulomb's Law,
$\begin{align*}F&=k\frac{Q_1.Q_2}{d^2}\\Q_A&=Q_B=Q\\F_A&=F_B=F=k\frac{Q^2}{d^2}\end{align*}$
When uncharged sphere C touches A, charge A distributes itself evenly:
$\begin{align*}Q_C=Q_A'=\frac{1}{2}Q_A=\frac{1}{2}Q\end{align*}$
When sphere C touches B:
$\begin{align*}Q_C'&=Q_B'=\frac{1}{2}Q_A\\&=\frac{1}{2}\left (Q_C+Q_B \right )\\&=\frac{1}{2}\left (\frac{1}{2}Q+Q \right )=\frac{3}{2}Q\end{align*}$
Therefore,
$\displaystyle \begin{align*}F_f&=k\frac{Q_1.Q_2}{r^2}\\&=k\frac{Q_A'.Q_B'}{r^2}\\&=k\frac{\frac{1}{2}Q.\frac{3}{4}Q}{r^2}\\&=\frac{3}{8}k\frac{Q^2}{r^2}=\frac{3}{8}F\end{align*}$
Answer: D
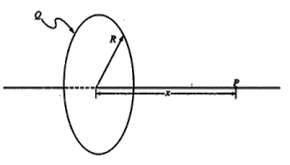
Problem 2: Theory, Problems and Solutions Electric Potential - Electromagnetism Question 3-4: refer to a thin, nonconducting ring of radius R, as shown below, which has a charge Q uniformly spread out on it.
One of the fundamental forces of the universe is the electric force. This is the force that exists between all charged particles.
Coulomb's law states that the electric force between two charged objects is directly proportional to the product of the sum of the charges on the objects and inversely proportional to the square of the distance between them.
In equation form, Coulomb's law can be expressed as
\[F=k\frac{Q_1.Q_2}{r^2}\]where
- $Q_1$ represents the amount of charge on body 1 (in Coulomb),
- $Q_2$ represents the amount of charge on object 2 (in Coulombs),
- r represents the distance between two objects (in meters).
- k is Coulomb's law constant. In air, $k=9.0 \times 10^9 Nm^2C^{-2}$.
Problem 1: Two balls of identical conductors, A and B, carry the same charge. The two are initially separated by a distance much larger than their diameter, and the force between them is F. The third identical conducting sphere, C, has no charge. Ball C is first touched to A, then to B, and then removed. Consequently, the force between A and B is equal to.
A. 0
B. $\displaystyle \frac{1}{6}F$
C. $\displaystyle \frac{1}{4}F$
D. $\displaystyle \frac{3}{8}F$
E. $\displaystyle \frac{1}{2}F$
Electric Force Solution:
Coulomb's Law,
$\begin{align*}F&=k\frac{Q_1.Q_2}{d^2}\\Q_A&=Q_B=Q\\F_A&=F_B=F=k\frac{Q^2}{d^2}\end{align*}$
When uncharged sphere C touches A, charge A distributes itself evenly:
$\begin{align*}Q_C=Q_A'=\frac{1}{2}Q_A=\frac{1}{2}Q\end{align*}$
When sphere C touches B:
$\begin{align*}Q_C'&=Q_B'=\frac{1}{2}Q_A\\&=\frac{1}{2}\left (Q_C+Q_B \right )\\&=\frac{1}{2}\left (\frac{1}{2}Q+Q \right )=\frac{3}{2}Q\end{align*}$
Therefore,
$\displaystyle \begin{align*}F_f&=k\frac{Q_1.Q_2}{r^2}\\&=k\frac{Q_A'.Q_B'}{r^2}\\&=k\frac{\frac{1}{2}Q.\frac{3}{4}Q}{r^2}\\&=\frac{3}{8}k\frac{Q^2}{r^2}=\frac{3}{8}F\end{align*}$
Answer: D
Problem 2: Theory, Problems and Solutions Electric Potential - Electromagnetism Question 3-4: refer to a thin, nonconducting ring of radius R, as shown below, which has a charge Q uniformly spread out on it.

A small particle of mass m and charge –q is placed at point P and released. If R ≫ x, the particle will undergo oscillations along the axis of symmetry with an angular frequency that is equal to:
A. $\begin{align*}\sqrt{\frac{qQ}{4\pi \epsilon _o{R}^3}}\end{align*}$
B. $\begin{align*}\sqrt{\frac{qQx}{4\pi \epsilon _om{R}^4}}\end{align*}$
C. $\begin{align*}\frac{qQ}{4\pi \epsilon _om{R}^3}\end{align*}$
A. $\begin{align*}\sqrt{\frac{qQ}{4\pi \epsilon _o{R}^3}}\end{align*}$
B. $\begin{align*}\sqrt{\frac{qQx}{4\pi \epsilon _om{R}^4}}\end{align*}$
C. $\begin{align*}\frac{qQ}{4\pi \epsilon _om{R}^3}\end{align*}$
D. $\begin{align*}\frac{qQx}{4\pi \epsilon _om{R}^4}\end{align*}$
E. $\begin{align*}\sqrt{\frac{qQx}{4\pi \epsilon _om{R}^4}}\left [\frac{1}{(R^2 + x^2)} \right ]\end{align*}$
E. $\begin{align*}\sqrt{\frac{qQx}{4\pi \epsilon _om{R}^4}}\left [\frac{1}{(R^2 + x^2)} \right ]\end{align*}$
Electric Force Solution:
$\begin{align*}F_{electric} &= k\frac{qQ}{r^2} \\F_{centripetal}&=m\frac{v^2}{r^2}=m\omega ^2r\\\end{align*}$
$\begin{align*}F_{e} &= F_{c}\\k\frac{qQ}{r^2}&=m\omega ^2r\\\omega ^2&=k\frac{qQ}{mr^3}\end{align*}$
with
$\begin{align*}k=\frac{1}{4\pi \epsilon _o} \end{align*}$
$\begin{align*}r^2=R^2 + x^2 \end{align*}$
$\begin{align*}R&>>x\\ r&^2\sim R^2 \Rightarrow r^3\sim R^3\end{align*}$
$\begin{align*}F_{electric} &= k\frac{qQ}{r^2} \\F_{centripetal}&=m\frac{v^2}{r^2}=m\omega ^2r\\\end{align*}$
$\begin{align*}F_{e} &= F_{c}\\k\frac{qQ}{r^2}&=m\omega ^2r\\\omega ^2&=k\frac{qQ}{mr^3}\end{align*}$
with
$\begin{align*}k=\frac{1}{4\pi \epsilon _o} \end{align*}$
$\begin{align*}r^2=R^2 + x^2 \end{align*}$
$\begin{align*}R&>>x\\ r&^2\sim R^2 \Rightarrow r^3\sim R^3\end{align*}$
so:
$\begin{align*}\omega =\sqrt{\frac{qQ}{4\pi \epsilon _o{R}^3}} \end{align*}$
Answer: A
$\begin{align*}\omega =\sqrt{\frac{qQ}{4\pi \epsilon _o{R}^3}} \end{align*}$
Answer: A
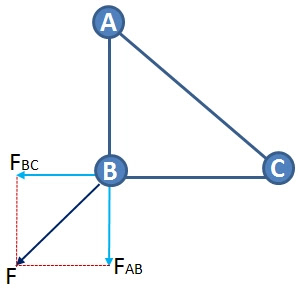
Problem 3: What is the magnitude and direction of the electric force on charge B according to the figure below?

Based on pictures:
- The object's charge A ($q_A$) = +Q
- Object charge B ($q_B$) = -2Q
- Object charge C ($q_C$) = -Q
- Distance between charges A and B ($r_{AB}$) = r
- Distance between charges B and C ($r_{BC}$) = 2r
- $k = 9\times 10^9 Nm^2C^{-2}$
asked:
The magnitude and direction of the electric force on charge B
Electric Force Solution:
Electric Force Solution:
The electric force between charges A and B :
$\begin{align*}F_{AB}&=\frac{k.q_A.q_B}{r_{AB}^2}\\&=\frac{k(Q)(2Q)}{r^2}\\&=\frac{2kQ^2}{r^2}\end{align*}$
The electric force between charge B and charge C:
$\begin{align*}F_{BC}&=\frac{k.q_B.q_C}{r_{BC}^2}\\&=\frac{k(2Q)(Q)}{2r^2}\\&=\frac{0,5kQ^2}{r^2}\end{align*}$
The net force acts on charge B
$\begin{align*}F &= F_{AB} + F_{BC}\\&=\frac{2kQ^2}{r^2}+\frac{0,5kQ^2}{r^2}\\&=\frac{2,5kQ^2}{r^2}\end{align*}$
Direction of the electric force towards charge A (to the left )
$\begin{align*}F_{AB}&=\frac{k.q_A.q_B}{r_{AB}^2}\\&=\frac{k(Q)(2Q)}{r^2}\\&=\frac{2kQ^2}{r^2}\end{align*}$
The electric force between charge B and charge C:
$\begin{align*}F_{BC}&=\frac{k.q_B.q_C}{r_{BC}^2}\\&=\frac{k(2Q)(Q)}{2r^2}\\&=\frac{0,5kQ^2}{r^2}\end{align*}$
The net force acts on charge B
$\begin{align*}F &= F_{AB} + F_{BC}\\&=\frac{2kQ^2}{r^2}+\frac{0,5kQ^2}{r^2}\\&=\frac{2,5kQ^2}{r^2}\end{align*}$
Direction of the electric force towards charge A (to the left )
Problem 4: Three charged particles A, B, and C are shown in the figure below. If AB = BC = 20 cm, the magnitude of the charges A, B and C is equal to q = 2µC
What is the magnitude of the electric force acting on charge B?
What is the magnitude of the electric force acting on charge B?
based on questions:
- Particle charge A: $\begin{align*}q_A=2\mu C = 2\times10^{-6} Coulomb \end{align*}$
- Particle charge B: $\begin{align*}q_B=2\mu C = 2\times10^{-6} Coulomb \end{align*}$
- Particle charge C: $\begin{align*}q_C=2\mu C = 2\times10^{-6} Coulomb \end{align*}$
- The distance from B to C: $\begin{align*}r_{BC}= 20 cm = 2\times10^{-6} meters \end{align*}$
- The distance from B to A: $\begin{align*}r_{BA}= 20 cm = 2\times 10^{-1}meters \end{align*}$
- $k = 9\times 10^9 Nm^2C^{-2}$
asked:
the magnitude of the electric force acting on charge B
Electric Force Solution:
The electric force between the charges at B and C:
$\begin{align*}F_{BC}&=\frac{k.q_A.q_B}{r_{AB}^2}\\&=9.10^9\frac{(2\times10^{-6} )(2\times10^{-6} )}{(2\times10^{-6})^2}\\&=0,9N \end{align*}$
The electric charges at point B and C are positive so that the direction of the electric force FBC to leftward away from point C.
The electric force between charges at A and B :
$\begin{align*}F_{AB}&=\frac{k.q_A.q_B}{r_{AB}^2}\\&=9.10^9\frac{(2\times10^{-6} )(2\times10^{-6} )}{(2\times10^{-6})^2}\\&=0,9N \end{align*}$
The electric charges at point B and A are positive so that the direction of the electric force FAB downward, away from point
$\begin{align*}F_{B}&= \sqrt{F_{AB}^2+F_{BC}^2}\\&= \sqrt{0,9^2+0,9^2}\\&=0,9 \sqrt{2}N\end{align*}$